Вітаю всіх з закінченням навчального року!
 Завдання на період 25.05-29.05
Завдання на період 25.05-29.05
Тема уроку:Повторення і узагальненя
Тема уроку:Повторення і узагальненя
матеріалу за рік.Контрольна робота за рік.
Завдання:
Оформити всі завдання, які не завершили.
Оформити всі завдання, які не завершили.
Повторити:
-Область визначення функції;
-Арифметична прогресія;
-Геометрична прогресія;
-Розв'язування нерівностей;
-Розв'язування систем рівнянь:
-Побудова графіка квадратичної функції
Підсумкова
контрольна робота з алгебри, 9 клас-Область визначення функції;
-Арифметична прогресія;
-Геометрична прогресія;
-Розв'язування нерівностей;
-Розв'язування систем рівнянь:
-Побудова графіка квадратичної функції
1.
Знайдіть усі
значення
, при яких має зміст вираз:
√(49-7x)
2. Розв’яжіть систему нерівностей:
{3x-15<0,
6x-2≥10.
3.
Чому дорівнює
знаменник геометричної прогресії
,якщо ,
b7=-3 b8=9
b7=-3 b8=9
4.
Скільки грамів солі міститься в 350г 4% розчину?
5. Розв’яжіть систему рівнянь:
{y2 -xy=12
3y-x=10
6. Знайдіть 30-ий
член арифметичної прогресії
, якщо
a5=9 a7=13
7.
Побудуйте графік функції
у = х2 +6х+8.
Користуючись графіком, знайдіть:
1) найменше значення функції;
2) проміжок, на
якому функція набуває додатних значень;
3) проміжок,
на якому функція спадає.
Завдання виконати до 29.05
Завдання на період 18.05-22.05
Завдання на 18.05
Тема уроку : Контрольна робота
Мета уроку: Перевірка рівня засвоєння
знань учнів з теми: "Геометрична прогресія"
Завдання: Контрольна робота
1. Яка з наведених послідовностей є
геометричною
прогресією? (1 бал)
А) 2; 6; 18; 36; Б) 80; 40; 20; 5;
А) 2; 6; 18; 36; Б) 80; 40; 20; 5;
В) 4; 8; 16; 32; Г) 2; -10; 50; 250.
2. Чому дорівнює четвертий член
геометричної
прогресії ( 1 бал),
якщо її перший член b1=6,
а знаменник
q=-2?
А) -48; Б) 48; В) 24; Г) -24.
А) -48; Б) 48; В) 24; Г) -24.
3. Знайдіть перший член геометричної прогресії
(1бал), якщо її другий член b2=-20,
а
знаменник q=-5.
А) 4; Б) -4; В) -100; Г) 100.
А) 4; Б) -4; В) -100; Г) 100.
4. Чому дорівнює сума нескінченної геометричної прогресії (1 бал),
перший член якої b1=18, а знаменник q=⅔?
А)
6; Б) 36; В) 54; Г) 48.
5. Знайдіть суму п’яти перших членів геометричної прогресії (bn) , якщо b3 = 5, b6 = 625. (2 бали)
6. Знайдіть суму всіх натуральних чисел, які кратні 6
і менші від 250. (3 бали)
7. При якому значенні х числа 2х-1, х+3, х+15 будуть послідовними
членами геометричної прогресії?
Знайдіть ці числа. (3 бали)
Завдання виконати до 19.05
Завдання на 19.05
Тема уроку: Корекція знань і вмінь учнів
Мета уроку: Аналіз та корекція допущених
типових помилок
Завдання: Повторити параграф 7 п.33-36
Виконати вправи :
Усно № 33.1, стор. 348
письмово №33.16,стор. 349
Завдання виконати до 20.05
Завдання на 20.05
Тема уроку: Повторення і
узагальнення матеріалу за рік
Мета уроку: Повторити тему: " Розв'язування систем рівнянь і нерівностей з двома змінними"
Завдання:Повторити параграф 4 п. 16-18
головне до параграфа 4, стор. 224.
виконати вправи : Зобразити на координатній площині множину розв'язків нерівності
№ 17.2(4); 17.4(1)
Довести нерівність №18.4(4)
Завдання виконати до 22.05
Завдання на 22.05
Тема уроку: Повторення і
узагальнення матеріалу за рік.
Мета уроку: Повторити тему: "Квадратична функція. Розв'язування квадратичних нерівностей."
Завдання:Повторити головне в параграф 2 , стор. 135-138 п.8-10
Розвязати нерівність методом інтервалів:
виконати вправи №10.2(1);10.12(2)
Завдання виконати до 25.05
Завдання на період 12.05-15.05
Завдання на 12.05
Тема уроку:Сума нескінченної геометричної прогресії
Мета уроку:Закріплення вмінь обчислювати суму нескінченної геометричної прогресії
Завдання: Повторити параграф 7 п.35

Формула суми нескінченної геометричної прогресії
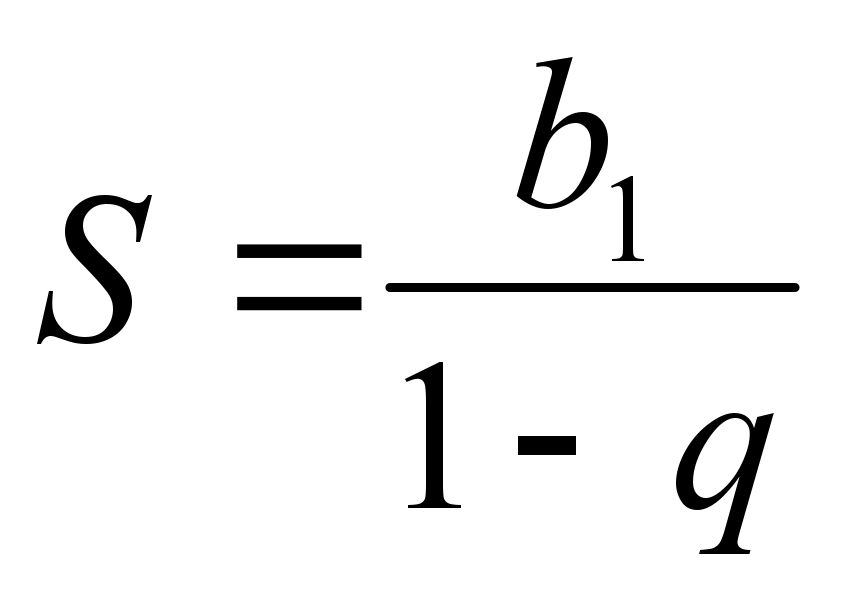
Використовуючи дані формули
виконати вправи
№35.10;35.15
Завдання виконати до 13.05
Завдання на 13.05
Тема уроку: Сумування послідовностей.
Мета уроку: Дати поняття сумування. Формувати вміння знаходити формулу n-го члена послідовності.
Завдання:
Опрацювати параграф 7 п.36 стор. 365
Розглянути зразки розв'язування прикладів
стор.366-368, приклади 1-6
Переглянути за посиланням :
Виконати вправу № 36.3
Завдання виконати до 15.05
Завдання на 15.05
Тема уроку: Узагальнення і систематизація знань.
Мета уроку: Повторити і узагальнити
знання з теми: "Геометрична прогресія"
Підготуватись до контрольної роботи.
Завдання:
Розглянути приклади розв'язування
основних задач на геометричну прогресію
1.Знайти знаменник і десятий член геометричної прогресії
(bn) : 2; –4; 8….
Розв'язання. (bn): 2; -4; 8;., то b1 = 2; b2 = -4, а q = b2 : b1; q = -4: 2 = -2;
b10 = b1q9; b10 = 2 ·(-2)9 = - 210
Відповідь: -2; -210.
2. Знайти знаменник геометричної прогресії (bn),
якщо b10 = 3, b12 = 12.
Розв'язання. Якщо b10 = 3; b12 = 12, то b12 = b10q2;
q2 = b12:b10; q2 = 12: 3 = 4; q1 = 2; q2 = -2.
Відповідь: -2 і 2.
3. Знайти шостий член і суму п’яти перших членів
геометричної прогресії (bn), якщо b1 = 7, q = 2.
Розв'язання. (bn): b1 = 7; q = 2, то b6 = b1q5;
b6 = 7· 25 = 7· 32 = 224.
За формулою суми n перших членів геометричної прогресії:
S5 = b1 (q5 - 1):(q - 1). S5 = 7·(25 -1):(2 - 1) = 7· 31 = 217.
Відповідь: b6 = 224; S5 = 217.
4. Послідовність (bn) є геометричною прогресією.
Знайдіть b5, якщо b4 = 9; b6 = 25.
Розв'язання. За властивістю геометричної прогресії,
b25 = b4·b6; b52 = 9·25; b1 = 3·5 = 15; b2 = -3·5 = -15.
Відповідь: -15 і 15.
5. Знайти суму шести перших членів геометричної прогресії (bn),
яка задана формулою bn = 2∙3n + 1.
Розв'язання. За умовою bn = 2·3n+1, то b1 = 2·31+1 = 2·32 = 2·9 =18,
а b2 = 2·32+1 = 2·33 =2·27 = 54. q = b2:b1; q = 54:18 = 3.
S6 = b1(q6 - 1):(q - 1). Отже, S6 = 18·(36 - 1):(3 - 1) =
9·(36 - 1) = 9·728 = 6552.
Відповідь: S6 = 6552.
6. Між числами 6 і 750 вставити два чисел так, щоб вони
разом із даними утворили геометричну прогресію.
Розв'язання. Якщо b1 = 6, а b4 = 750, то b4 = b1q3,
q3 = 750:6 = 125; q = 5. Отже, b2 = b1q; b2 = 6·5 = 30;
b3 = b1q; b3 = 30·5 = 150.
Відповідь: 30 і 150.
7. Утворити геометричну прогресію (bn), якщо
різниця другого та першого її членів дорівнює -4,
а різниця третього та першого дорівнює 8.
Розв'язання. Якщо b2 - b1 = -4,а b3 - b1 = 8,
то утворивши систему з даних рівнянь та розв'язавши її,
ми знайдемо q =-3; b1 = 1.
Повторити параграф 7 п. 34-36.
Підготуватись до контрольної рботи
Завдання виконати до 18.05
Завдання на період 04.05-08.05
Завдання на 04.05
Завдання на 05.05
Тема
уроку :Сума n -перших
членів геометричної прогресії.
Мета уроку: Вивести формулу суми n
-перших членів геометричної прогресії.Формувати вміння застосовувати її
для знаходження сум
Завдання:
Переглянути за посиланням :
2.формула суми (приклади)
Опрацювати параграф 7 п.34
виписати формули
Виконати вправи № 34.12; №34.21
Завдання виконати до 06.05
Завдання на 06.05
Тема уроку:Уявлення про границю послідовності. Сума нескінченної геометричної прогресії, у якої ІqІ < 1
Мета уроку:Дати поняття границі послідовності;збіжної послідовності;
суми нескінченної геометричної прогресії.
Завдання:Переглянути за посиланням:
геометричної прогресії - теоретичний орієнтир
геометричної прогресії- приклади
Опрацювати параграф 7, п.35
Виписати формули,
Розглянути приклади 1-3 на стор. 360-361
Виконати вправи №35.2;35.12
Завдання виконати до 08.05
Завдання на 08.05
Тема уроку:Сума нескінченної геометричної прогресії
Мета уроку:Закріплення вмінь обчислювати суму нескінченної геометричної прогресії
Завдання:
Повторити параграф 7 П.35
Виконати вправи №35.17;№35.25
Завдання виконати до 12.05
Завдання на період 27.04-01.05
Завдання на 27.04
Тема уроку: Контрольна робота з теми: "Числові послідовності. Арифметична прогресія"
Мета уроку: Перевірка рівня знань учнів з теми: "Числові послідовності. Арифметична прогресія"
Завдання :
Контрольна робота
Контрольна робота
- Тема уроку:Корекція знань, умінь і навичок з теми:"Числові послідовності. Арифметична прогресія"
- Мета уроку:Прокоментувати помилки, допущені при виконанні контрольної роботи.Зкорегувати учнів на правильне вирішення проблеми.
- Завдання: Повторити параграф 30 П. 30-33
- Проаналізуйте зроблені помилки, та перегляньте зразки розв'язку деяких завдань
- Приклад1: Знайдемо а9, якщо (аn) — арифметична прогресія, перші члени якої: 7,8; 8,9; 10; ....Розв'язання:Знайдемо різницю арифметичної прогресії, у якої а1 = 7,8; a2 = 8,9; a3 = 10: d = a3 – a2 = 10 – 8,9 = 1,1.Формула n-го члена арифметичної прогресії має вигляд an = a1 + d(n – 1).Враховуючи, що а1 = 7,8, d = 1,1, маємо: аn = 7,8 + 1,1(n – 1).Отже, а9 = 7,8 + 1,1(9 – 1) = 7,8 + 8,8 = 16,6.Відповідь: а9 = 16,6.
- Приклад 2:Дев'ятий член арифметичної прогресії дорівнює 23. Чому дорівнює сума восьмого і десятого членів цієї прогресії?
- Розв'язання. Запишемо формули восьмого і дев'ятого члена арифметичної прогресії через 9 її член
a[10]=a[9]+d;
a[9]=a[8]+d;
a[8]=a[9]-d.
Знайдемо суму двох членів прогресії
a[8]+ a[10]= a[9]-d +a[9]+d=2*a[9].
Виконуємо обчислення
S=2*23=46.
Запам'ятайте, що кожен член арифметичної прогресії може бути визначений як середнє арифметичне сусідніх
Правило діє незалежно від того наскільки вони віддалені від нього
Формули досить часто застосовують в обчисленнях, тому постарайтеся їх вивчити. - Приклад3:Знайдіть суму натуральних чисел, кратних 7 і не більших від 145.
- Розв'язання. Числа кратні 7 означає, що різниця прогресії рівна d=7. Обчислимо кiлькiсть таких чисел діленням 145/7=20 цілих і 5 остачі.Тоді останній доданок суми рівний a[20]=20*7=140. Обчислюємо суму арифметичної прогресії S=(7+140)*20/2=1470.
- Розв'яжіть задачі:1. Знайдіть перші чотири члени арифметичної прогресії (аn), якщо а1 = 1,2, d = -0,1.2. Знайдіть різницю і сотий член арифметичної прогресії (аn): 2,7; 3,1; 3,5; ... .3. Між числами -4 і 5 вставте п'ять таких чисел, щоб вони разом із даними числами утворювали арифметичну прогресію.4. Дана арифметична прогресія: 2; 1,8; 1,6; ... . Знайдіть її найбільший від'ємний член.
Завдання виконати до 29.04
Завдання на 29.04
Тема уроку:Геометрична прогресія та її властивості. Формула n-го члена геометричної прогресії.
Мета уроку: Дати поняття геометричної прогресії. Навчити знаходити знаменник геометричної прогресії , та за формулою n-го члена будь-який член прогресії.
Тема уроку:Геометрична прогресія та її властивості. Формула n-го члена геометричної прогресії.
Мета уроку: Дати поняття геометричної прогресії. Навчити знаходити знаменник геометричної прогресії , та за формулою n-го члена будь-який член прогресії.
Завдання: Переглянути за посиланням:
відеоурок Геометрична прогресія. Формула n-го члена геометричної прогресії.
Опрацювати зміст параграфа7 п.33
Виписати формули.
Виконати вправи :
Усно №33.1
Письмово №33.8; 33.14(2)
відеоурок Геометрична прогресія. Формула n-го члена геометричної прогресії.
Опрацювати зміст параграфа7 п.33
Виписати формули.
Виконати вправи :
Усно №33.1
Письмово №33.8; 33.14(2)
Завдання виконати до 01.05
Завдання на період 21.04-24.04
Завдання на 21.04
Тема уроку: Арифметична прогресія, її властивості. Формула суми n- членів арифметичної прогресії.
Мета уроку: Розвиток навичок використання формули суми n-членів арифметичної прогресії. Закріплення знань.Розв'язування вправ.
Завдання: Повторити параграф 32.
Формули . Виконати вправи:
№ 32.16; 32.18;
Завдання виконати до 22.04
Завдання на 22.04
Тема уроку: Арифметична прогресія, її властивості. Формула суми n- членів арифметичної прогресії.
Мета уроку:Закріплення знань використання формули суми n- членів арифметичної прогресії.Розв'язування вправ
Завдання: Повторити параграф 32.
Формули . Виконати вправи:
№32.29;32.33
Завдання виконати до 24.04
Формули . Виконати вправи:
№32.29;32.33
Завдання виконати до 24.04
Завдання на 24.04
Тема уроку: Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії.Формула суми n- членів арифметичної прогресії.
Мета уроку: Узагальнення і систематизація знань з теми :"Арифметична прогресія"
Завдання:
Повторити і узагальнити зміст параграфів 30-32.
Повторити і узагальнити зміст параграфів 30-32.
1. Задана скінченна послідовність: (аn): 2; -1; 5; -2; 9; -3; 15; -4. Знайдіть суму:
1) перших двох її членів;
2) перших п'яти її членів;
3) усіх її членів.
2. Знайдіть суму перших тридцяти членів арифметичної прогресії (хп), у якої х1 = 5, х30 = 15.
3. Знайдіть суму перших десяти членів арифметичної прогресії (уп), у якої y1 = 5, d = 3, заповнивши пропуски у формулі 
4. В арифметичній прогресії (ап) а1 = 1, d = 4.
Знайдіть а10, S10.
5. Дано арифметичну прогресію (аn). Знайдіть:
1) п, якщо a1 = 5, an = 25, Sn = 150;
2) a1, якщо d = 2, n = 4, S4 = 10.
6. Виразіть із формули  :
:
1) a1; 2) ап.
Завдання виконати до 27.04
Завдання на період з 13.04 - 17.04
Завдання на 13.04:
Тема уроку: Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії
Мета уроку: Сформувати поняття арифметичної прогресії, формули n-го члена арифметичної прогресії. Навчити учнів за допомогою рекурентної формули знаходити невідомий член арифметичної прогресії
Завдання:Переглянути відеоурок
Опрацювати параграфи 30-31 , виписати формули в робочий зошит, виконати вправи
№№ 30.3;30.6;30.16
Завдання виконати до 14.04
Завдання на 14.04
Тема уроку: Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії
Мета уроку :Розширити та поглибити знання учнів з теми "Арифметична прогресія. .Формула n-го члена арифметичної прогресії.
Завдання:
Повторити параграф 31.
Виконати вправи № 31.2, №31.4, №31.7, №31.10, №31.12
Завдання виконати до 15.04
Завдання на 15.04
Тема уроку: Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії
Мета уроку :Розширити та поглибити знання учнів з теми "Арифметична прогресія. .Формула n-го члена арифметичної прогресії.
Завдання:
Повторити параграф 31.
Виконати вправи № 31.14,№31.24
Завдання виконати до 17.04
Завдання на 17.04
Тема уроку: Сума n-перших членів
арифметичної прогресії
Мета уроку:Вивести формулу для обчислення суми членів арифметичної прогресіі та навчити учнів використовувати її на практиці.
Завдання :
Переглянути відеоурок
Опрацювати Параграф 32. Виписати формули. Виконати вправи №32.2, №32.4, №32.8,№32.10
Завдання виконати до 20.04
Немає коментарів:
Дописати коментар